tech-lessons.in
Background by Fernando Paredes Murillo on Unsplash
February 24, 2023

Count-min sketch

Posted on February 24, 2023  •  11 minutes  • 2339 words
Table of contents

Count-min sketch (CM sketch) is a probabilistic data structure1 used to estimate the frequency of events in a data stream.

It relies on hash functions to map events to frequencies, but unlike a hash table, it uses only sublinear space at the expense of over-counting some events due to hash collisions. The count–min sketch was invented in 2003 by Graham Cormode and S. Muthu Muthukrishnan.

Understanding Count-min Sketch

Let’s say we want to build a solution to count the frequency of elements in a data stream. One idea would be to use a hashmap with the data element as the key and count as the value. The approach works but does not scale with a data stream comprising billions of elements, the most unique.

We will have two challenges with hashmap in this case:

  1. The number of elements in the hashmap will tend towards a billion. The overall space complexity would be O(N)2
  2. Rehashing can place significant CPU pressure

This is where the Count-min sketch comes into the picture. The count-min sketch is a probabilistic data structure that can estimate the frequency of elements by using sublinear space at the expense of over-counting some elements due to hash collisions.

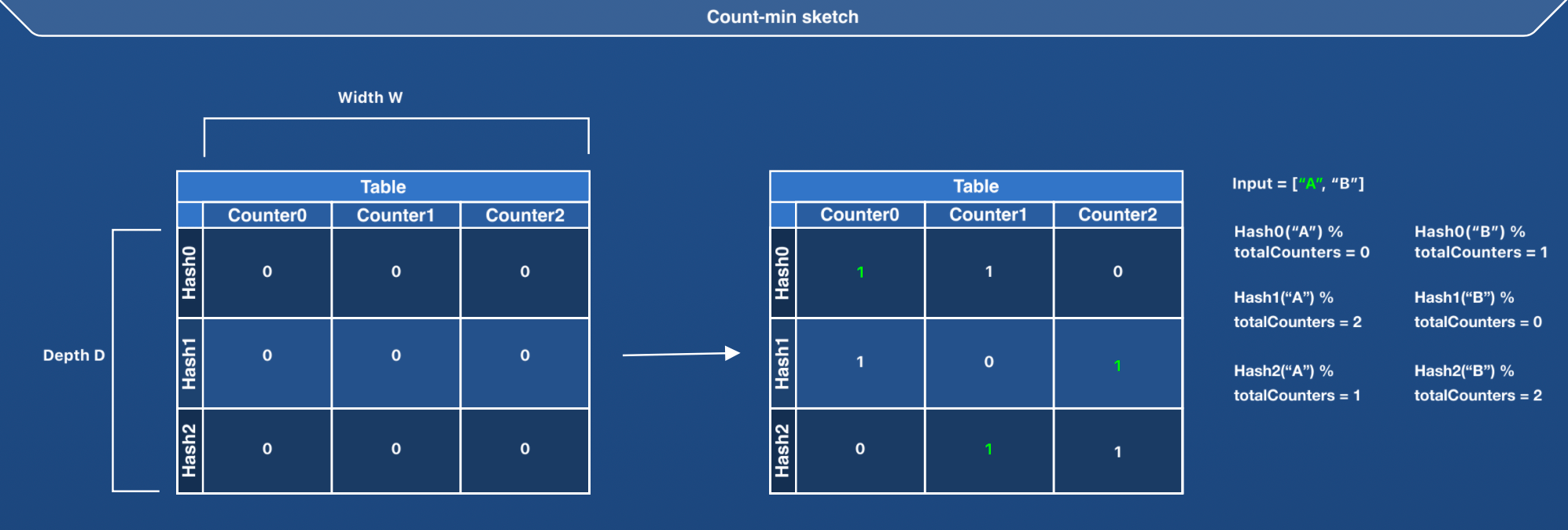
Count-min sketch is represented as a D*W matrix, where D is the total number of hash functions (or depth) and W is the width or the number of counters per hash function. The matrix is initialized with zero at the beginning. A count-min sketch can be represented with the following structure:

const depth = 4

type CountMinSketch struct {
    matrix        [depth]row
    seeds         [depth]uint64
    totalCounters uint64
}

type row []byte

CountMinSketch contains the following:

  1. A matrix of a byte array to store the counters. Each row will have W cells, and each cell will contain a byte.
  2. The total number of rows (or the total number of hash functions) is limited to four in the above code. So, D here is 4.
  3. An array of seed values of type uint64 will be used to generate the hash of the data element.
  4. Total number of counters

We plan to use a “four-bit counter” approach, with the lower four bits of a byte to store the counter for a key K1 and the upper four bits to hold the counter for another key K2. That means a byte will store the counts for two keys.

From now on, we will use the term “key” over “data element”. Count-min sketch supports two operations - increment(key) and estimate(key). Let’s understand the working of these operations.

The idea behind the increment operation can be summarized as follows:

  1. Run D hash functions on the given key (hash0, hash1 and hash2 in the image above).
  2. Find a column index in the matrix by performing hashValue % totalCounters.
  3. Increment the value at the identified matrix cell using four-bit counter approach .

The idea behind the estimate operation is similar to the increment operation.

  1. Run D hash functions on the given key (hash0, hash1 and hash2 in the above image).
  2. Find a column index in the matrix by performing hashValue % totalCounters.
  3. Return the minimum value from all the identified matrix cells.

We return the minimum value from all the identified matrix cells to account for hash conflicts between keys. 2 keys might get the same column index (hashValue % totalCounters) for the 0th row, but they might get different column indices for the 1st row. So, we take the minimum counter value from all the identified matrix cells to reduce the impact of hash conflicts between keys.

Adding tests for increment and estimate

Let’s add a test for increment and estimate operations.

func TestGetsTheEstimateForKeysInAStream(t *testing.T) {
    stream := []model.Slice{
        model.NewSlice([]byte("A")), 
        model.NewSlice([]byte("B")),
        model.NewSlice([]byte("A")), 
        model.NewSlice([]byte("C")),
        model.NewSlice([]byte("B")), 
        model.NewSlice([]byte("A")),
        model.NewSlice([]byte("B")), 
        model.NewSlice([]byte("C")),
    }
    expectedCounts := map[string]byte{
        "A": 3,
        "B": 3,
        "C": 2,
    }

    //instantiate countMinSketch with ten counters
    countMinSketch := newCountMinSketch(10)

    //increment
    for _, key := range stream {
        countMinSketch.Increment(key)
    }

    //estimate the count
    for _, key := range stream {
        count := countMinSketch.Estimate(key)
       if count < expectedCounts[key.AsString()] {
                t.Fatalf(
                    "Expected at least the count %v for key %v, received %v", 
                    expectedCounts[key.AsString()], 
                    key.AsString(), 
                    count
                )
        }
    }
}

Let’s quickly understand the test:

  1. Create a stream of keys. Keys are represented by the Slice abstraction, which is a wrapper over a byte slice.
  2. Create a count-min sketch with ten counters (width as 10)
  1. Increment the count for all the keys in the stream.
  2. Assert the estimate of count for all the keys

As a part of the assertion, we want to ensure that the estimated count is “at least” equal to the expected count. In the case of hash collisions between two keys, an estimate of the count might be higher than the expected count. Hence, we hope that the estimated count is “at least” equal to the expected count.

4-bit counter

The idea behind the four-bit counter deserves its mention.

Now is the right time to build a count-min sketch.

Building Count-min sketch

Let’s understand the critical aspects of newCountMinSketch function.

const depth = 4

type row []byte

type CountMinSketch struct {
   matrix        [depth]row
   seeds         [depth]uint64
   totalCounters uint64
}

func newCountMinSketch(counters int) *CountMinSketch {
    nextPowerOf2 := func(counters int64) int64 {
        counters--
        counters |= counters >> 1
        counters |= counters >> 2
        counters |= counters >> 4
        counters |= counters >> 8
        counters |= counters >> 16
        counters |= counters >> 32
        counters++
        return counters
    }

    //initialize the source to generate seed values and set the total counters to be a power of 2
    //if the user-specified counter is 10, we get a total of 16 counters
    source, updatedCounters := rand.New(rand.NewSource(time.Now().UnixNano())), nextPowerOf2(int64(counters))

    //instantiate CountMinSketch
    countMinSketch  := &CountMinSketch{totalCounters: uint64(updatedCounters)}

    for index := 0; index < depth; index++ {
        //generate a new seed
        countMinSketch.seeds[index] = source.Uint64()
        //create a new byte array using the make function and set the newly created byte array at the current index of the matrix
        countMinSketch.matrix[index] = make(row, updatedCounters/2) 
    }
    return countMinSketch
}

The idea behind newCountMinSketch can be summarized as follows:

  1. Create a new source for generating seed values and set the counter as a power of 2.
  2. Set totalCounters inside CountMinSketch
  3. Iterate from index = 0 to depth-1 and do the following:

Every row in the matrix has a byte array of size updatedCounters/2. Using the four-bit counter approach, each byte stores the counters for two keys. This means that we can reduce the total number of counters by 2. With the input counter as 18, we get the value of updatedCounters as 32. Using the four-bit counter approach, we end up with 16 cells (32/2) for each row, with each cell containing a byte.

The idea behind Increment can be summarized as follows:

  1. Iterate from index = 0 to depth-1 and do the following:

Increment operation will increment either the upper or lower four bits of the byte depending on the matrix cell position.

This is how the above approach can be implemented in golang:

func (countMinSketch *CountMinSketch) Increment(key model.Slice) {
    for index := 0; index < depth; index++ {
        //compute the hash value
        hash        := countMinSketch.runHash(key, uint32(countMinSketch.seeds[index]))
        //get the current row (instance of type row is an alias for []byte)
        currentRow  := countMinSketch.matrix[index]
        //increment the value from the current row at an index=hash % countMinSketch.totalCounters
        currentRow.incrementAt(hash % countMinSketch.totalCounters)
    }
}
func (currentRow row) incrementAt(position uint64) {
    //get the index
    index := position / 2
    //if the position is an odd number, upper four bits store the counter value,
    //else lower four bits store the counter value
    shift := (position & 0x01) * 4    
    isLessThan15 := (currentRow[index]>>shift)&0x0f < 0x0f
    //if the value is less than 15, increment
    if isLessThan15 {
       currentRow[index] = currentRow[index] + (1 << shift)
    }
}

The idea behind Estimate can be summarized as follows:

  1. Iterate from index = 0 to depth-1 and do the following:

This is how the above approach can be implemented in golang:

func (countMinSketch *CountMinSketch) Estimate(key model.Slice) byte {
   min := byte(255)
    for index := 0; index < depth; index++ {
        //compute the hash value
        hash       := countMinSketch.runHash(key, uint32(countMinSketch.seeds[index]))
        //get the current row (an instance of type row is an alias for []byte)
        currentRow := countMinSketch.matrix[index]
        //get the value from the current row at an index=hash % countMinSketch.totalCounters and find the minimum value 
        if valueAt := currentRow.getAt(hash % countMinSketch.totalCounters); valueAt < min {
            min = valueAt
        }
    }
    return min
}
func (currentRow row) getAt(position uint64) byte {
    //get the index
    index := position / 2
    //if the position is an odd number, the upper four bits store the counter value,
    //else lower four bits store the counter value
    shift := (position & 0x01) * 4
    //perform the shift (shift would be either 0 or 4) 
    //perform an AND operation with 0x0f, which 00001111
    return (currentRow[index] >> shift) & 0x0f
}

Let’s understand how Ristretto uses count-min sketch.

Ristretto

Ristretto is a fast, concurrent golang cache library built with a focus on performance and correctness. Ristretto development team set the following requirements for the cache:

  1. It should support concurrency
  2. It should maintain a high cache-hit ratio
  3. It should be memory-bounded (limit to configurable max memory usage)
  4. It should scale well as the number of cores and goroutines increases
  5. It should scale well under non-random key access distribution (e.g. Zipf)

One of the exciting requirements was “maintaining a high cache-hit ratio”. To achieve this goal, the development team implemented an LFU (least frequently used) based eviction policy called TinyLFU .

TinyLFU is an eviction-agnostic admission policy designed to improve hit ratios with very little memory overhead. The main idea is only to let in a new element if its estimate (/cost) exceeds the item being evicted. Ristretto implements TinyLFU using count-min sketch that uses four-bit counter .

Let’s look at a code snippet from Ristretto.

Ristretto’s tinyLFU (policy.go) references cmSketch which implements count-min sketch.

type tinyLFU struct {
    freq    *cmSketch
    //fields omitted
}

func (tinyLFU *tinyLFU) Push(keys []uint64) {
    for _, key := range keys {
        tinyLFU.Increment(key)
    }
}

//code omitted
func (tinyLFU *tinyLFU) Increment(key uint64) {
    tinyLFU.freq.Increment(key)
}

//code omitted
func (tinyLFU *tinyLFU) Estimate(key uint64) int64 {
    hits := tinyLFU.freq.Estimate(key)
    return hits
}

Any access to a key in an LFU-based caching solution should increment the frequency of the accessed key. Instead of implementing the accurate key access count, Ristretto decided to use an estimated access count.

To increase the access count of a key, Ristretto batches the gets in a buffer. When the buffer is full, the buffered keys are handed off to a goroutine for incrementing their frequencies. This is why the Push method of tinyLFU receives a slice of keys of type uint64 (hash of the incoming keys).

The Push method results in incrementing the access frequency of the keys by invoking the Increment method on the cmSketch object. cmSketch (sketch.go) is an implementation of the count-min sketch.

With Ristretto, keys are already hashed, so the type of the parameter for the key in all these methods is uint64.

tinyLFU also provides a method called Estimate responsible for estimating a given key’s frequency. To get the estimate, tinyLFU invokes the Estimate method on the cmSketch object and returns the estimated frequency of the key.

Code

The code for this article is available here .

Mention

Thank you, Debasish Ghosh for reviewing the article and providing feedback.

References

  1. Probabilistic data structures provide approximate answers to queries about a large dataset rather than exact answers. These data structures are designed to handle large amounts of data in real-time by making trade-offs between accuracy and time and space efficiency. ↩︎

  2. Big O notation In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. ↩︎

Count-min sketch

Probabilistic data structure