tech-lessons.in
Background by Drift Shutterbug on Pexels
May 26, 2023

Designing an in-memory LFU cache

Posted on May 26, 2023  •  21 minutes  • 4278 words
Table of contents

I had been working on building an in-memory LFU cache (least frequently used cache) and now that it is done, I thought of writing about the building blocks of an LFU cache. This article shares the building blocks of an LFU cache along with the ideas from two research papers: TinyLFU and BP-Wrapper

CacheD is the name of my cache, and it is inspired by Ristretto . I know CacheD is a very creative name. Thank you.

Let’s get started.

LFU cache

According to Wikipedia : Least Frequently Used (LFU) is a type of cache algorithm used to manage memory within a computer. The standard characteristics of this method involve the system keeping track of the number of times a block is referenced in memory. When the cache is full and requires more room the system will purge the item with the lowest reference frequency.

Let’s now understand the building blocks of an LFU cache, starting with a way to measure the access frequency.

Measuring access frequency

All LFU caches need to maintain the access frequency for each key. Storing the access frequency in a HashMap-like data structure would mean that the space used to store the frequency is directly proportional to the number of keys in the cache. This is an opportunity to use a probabilistic data structure like count-min sketch and make a trade-off between the accuracy of the access frequency and the space used to store the frequency.

Count-min sketch (CM sketch) is a probabilistic data structure that estimates the frequency of events in a data stream. It relies on hash functions to map events to frequencies, but unlike a hash table, it uses only sublinear space at the expense of over-counting some events due to hash collisions. The count–min sketch was invented in 2003 by Graham Cormode and S. Muthu Muthukrishnan.

CacheD uses count-min sketch inside the abstraction FrequencyCounter to store the frequency for each key.

Count-min sketch is represented as a D*W matrix, where D is the total number of hash functions (or depth) and W is the width or the number of counters per hash function.

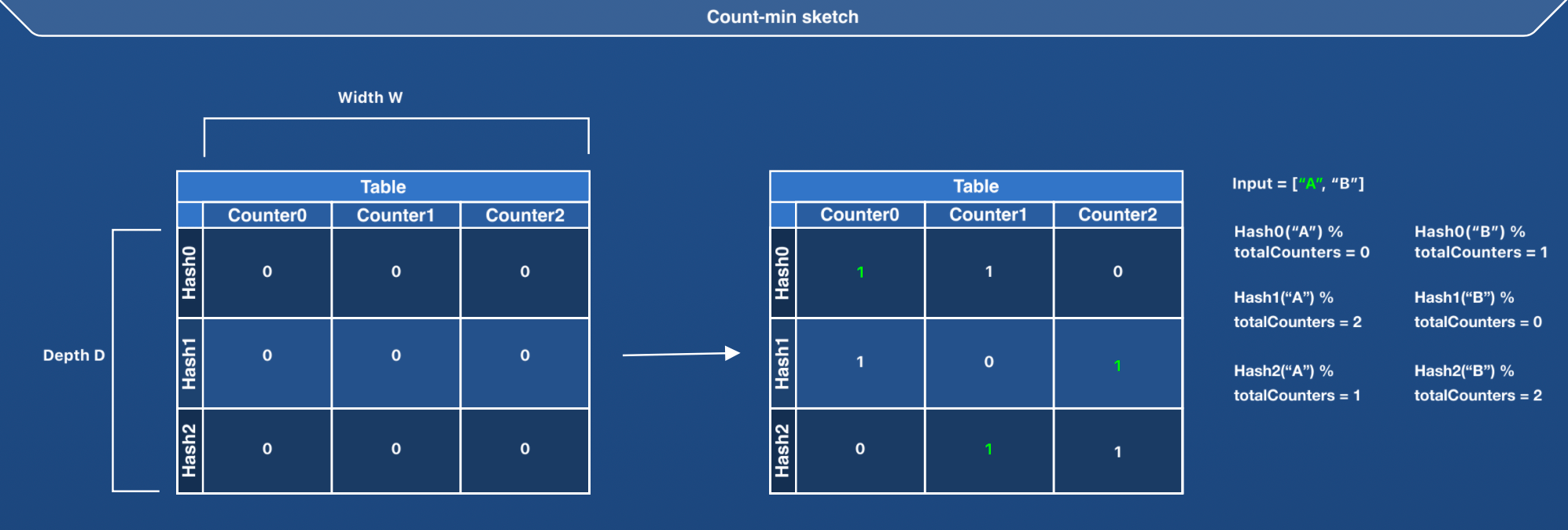
The matrix is initialized with zero at the beginning. A count-min sketch can be represented with the following structure:

#[repr(transparent)]
#[derive(Debug, PartialEq)]
struct Row(Vec<u8>);

const ROWS: usize = 4;

pub(crate) struct FrequencyCounter {
    matrix: [Row; ROWS],
    seeds: [u64; ROWS],
}

//initialize the matrix
fn matrix(total_counters: TotalCounters) -> [Row; ROWS] {
    let total_counters = (total_counters / 2) as usize;
    let rows =
        (0..ROWS)
            .map(|_index| Row(vec![0; total_counters]))
            .collect::<Vec<Row>>();

    rows.try_into().unwrap()
}

We still need to decide on the number of counters. What should the number of counters be to get the closest access frequency estimate?

We can start with a simple theory. If an LFU cache contains N keys, we can keep N counters per hash function in the count-min sketch. However, we need to consider hash conflicts.

Let’s understand the logic of incrementing the access frequency of a key with the following pseudocode.

    pub(crate) fn increment_access_for(&self, key: Key) {
        // 1) Iterate through all the rows (row = 0 to depth = D)
        // 2) Get the hash of the incoming key
        // 3) Perform `hash % self.total_counters` to identify the column index (with width = W)
        // 4) Increment the value at the identified column in the row R(i)
    }

Keeping the counters (imagine them as the number of columns) the same as the number of keys in the cache would mean a higher error rate in the access frequency estimate (because of hash conflicts).

To keep the estimates from wavering (/overestimating) too much because of hash conflicts, we need to have counters = K times the number of keys. Any choice of K is an attempt at reducing the hash conflict of keys in each row.

CacheD proposes K = 10 and does performance benchmarks with K = 2 and K = 10.

We have a way of measuring the access frequency of each key. Let’s understand a way to store the key/value mapping.

Storing key/value mapping

We need a way to store the value by key. This is done by the Store abstraction in Cached. Store uses DashMap , a concurrent associative array/hashmap.

DashMap maintains an array named shards; each element is a RwLock to a HashMap. The put operation for a key identifies the shard_index, acquires a write lock against that shard and writes to the HashMap in the identified shard.

pub struct DashMap<K, V, S = RandomState> {
    shards: Box<[RwLock<HashMap<K, V, S>>]>,
    //code omitted
}

We are build our key/value mapping on top of DashMap. The following code represents Store.

pub(crate) struct Store<Key, Value>
    where Key: Hash + Eq, {
    store: DashMap<Key, StoredValue<Value>>,
}

pub struct StoredValue<Value> {
    value: Value,
    key_id: KeyId,
    expire_after: Option<ExpireAfter>,
    pub(crate) is_soft_deleted: bool,
}

There is another decision to be made here.

How should we return the value to the clients as a part of the get operation?

Let’s look at Option 1 first. To return a reference to the value, we need to look into the get method of DashMap.

pub fn get<Q>(&'a self, key: &Q) -> Option<Ref<'a, K, V, S>>
where
    K: Borrow<Q>,
    Q: Hash + Eq + ?Sized, { self._get(key) }

pub struct Ref<'a, K, V, S = RandomState> {
    _guard: RwLockReadGuard<'a, HashMap<K, V, S>>,
    k: *const K,
    v: *const V,
}

pub type RwLockReadGuard<'a, T> = lock_api::RwLockReadGuard<'a, RawRwLock, T>;

//part of lock_api
pub struct RwLockReadGuard<'a, R: RawRwLock, T: ?Sized> {
    rwlock: &'a RwLock<R, T>,
    marker: PhantomData<(&'a T, R::GuardMarker)>,
}

This means if we decide to return a reference to the value for a key, we are actually returning DashMap's Ref and also holding a lock against the shard that the key belongs to.

The Store abstraction in CacheD provides get_ref method that returns an instance of KeyValueRef which wraps DashMap's Ref.

pub(crate) fn get_ref(&self, key: &Key) -> Option<KeyValueRef<'_, Key, StoredValue<Value>>> {...}

pub struct KeyValueRef<'a, Key, Value>
    where Key: Eq + Hash {
    key_value_ref: Ref<'a, Key, Value>,
}

At the same time, Store provides get method if the value is cloneable, which returns an Option<Value>. This behavior will cause DashMap to hold the lock against the shard while the value is being read, clone the value, return the value to the client, and drop the lock. This is a tradeoff (of sorts) in both the methods: get_ref and get.

impl<Key, Value> Store<Key, Value>
    where Key: Hash + Eq,
          Value: Clone, {
    pub(crate) fn get(&self, key: &Key) -> Option<Value> {
        let maybe_value = self.store.get(key);
        let mapped_value = maybe_value
            .filter(|stored_value| stored_value.is_alive(&self.clock))
            .map(|key_value_ref| { key_value_ref.value().value() }); //clone the value

        mapped_value
    }
}

Let’s bring another requirement: “memory bound cache”.

Making the cache memory bound

We want to design a cache that uses a fixed amount of memory determined by some configuration parameter.

This requirement brings in two concepts:

  1. Every key/value pair should take some size, and we should be able to determine the total size used by the cache.
  2. We must ensure the total cache size does not exceed the specified limit.

CacheD uses the term “weight” to denote the space (/size).

Let’s understand the first point.

To associate weight with each key/value pair, we can provide a variant of the put method that takes weight as a parameter along with key and value. Cached provides a method put_with_weight() that allows the clients to specify the weight associated with each key/value pair.

Another option is to auto-calculate the weight for each key/value pair. To calculate the weight, we should be able to calculate the size of each key/value pair using functions like std::mem::size_of_val() or std::mem::size_of() and adding to that the size of any additional metadata, like expiry: Duration, that might be stored for each key/value pair.

The weight calculation in CacheD is available here .

Now that we have calculated the weight of each key/value pair, we should maintain the weight of each key and the total weight used by the cache.

CacheD uses CacheWeight as an abstraction to maintain the weight of each key in the cache, and it also keeps the total weight used by the cache. The weight of each key is maintained via the WeightedKey abstraction that contains the key, key_hash and its weight. Every put increases the cache weight, every delete reduces the cache weight, and every update probably changes the cache weight.

pub(crate) struct CacheWeight<Key>
    where Key: Hash + Eq + Send + Sync + Clone + 'static, {
    max_weight: Weight,
    weight_used: RwLock<Weight>,
    key_weights: DashMap<KeyId, WeightedKey<Key>>,
}

We have the weight associated with each key/value pair.

Admission and eviction policy

Our cache is a memory-bound cache, and this poses an exciting challenge.

Should we admit the incoming key/value pair after the cache has reached its weight? If yes, which keys should be evicted to create the space because we can not let the total cache weight increase beyond some threshold?

This is where the paper TinyLFU comes into the picture. The main idea is to only let in a new key/value pair if its access estimate exceeds that of the item being evicted. This means that the incoming key/value pair should be more valuable to the cache than some existing key/value pairs, improving the hit ratio.

Let’s look at the approach:

Approach:

  1. Get an estimate of the access frequency of the incoming key. The incoming key has not been accessed yet, but we might get some access count because of hash conflicts since we rely on the probabilistic data structure count-min sketch to maintain the access frequencies of the keys.
  2. Get a sample of the existing keys (from CacheWeight) that consists of keyId, its weight and its access frequency. Sample size can be configurable.
  3. Pick the key with the smallest access frequency from the sample. Let’s call this key K1.
  4. If the access frequency of the incoming key is less than the access frequency of the key K1, then reject the incoming key because its access frequency is less than the smallest access frequency in the sample.
  5. Else, delete the key K1 and create the space in the cache. The space created will be equal to the weight of K1.
  6. Repeat the process until either the incoming key is rejected or enough space to accommodate the incoming key is created in the cache.

This approach is called “Sampled LFU”. CacheD uses AdmissionPolicy abstraction to decide whether an incoming key/value pair should be admitted.

There is still one more case to consider. What if there is a key with high access frequency, and it has been a while since it has been seen. Will it never get evicted?

This point is around the recency of key access. The TinyLFU abstraction ensures the recency of key access by the reset method. We have used count-min sketch to maintain each key’s access frequency; every time a key is accessed, the frequency counter is incremented. After N key increments, the counters get halved. So, a key that has not been seen for a while would also have its counter reset to half of the original value; thereby providing a chance to the new incoming keys to get in. *TinyLFU paper section: Freshness Mechanism

The abstraction TinyLFU has a FrequencyCounter and a DoorKeeper . DoorKeeper is implemented using a Bloom filter . Before increasing the access frequency of a key in FrequencyCounter, a check is done in the DoorKeeper to see if the key is present. Only if the key is present in the DoorKeeper, its access count is incremented. This ensures that FrequencyCounter does not have a long tail of keys that are not seen more than once.

Our cache is concurrent, so let’s understand how to deal with contention.

Introducing BP-Wrapper

We have already seen Store and count-min sketch based FrequencyCounter. Technically, both are shared data structures prone to contention .

Let’s understand this with an example. Imagine there is a get request for an existing key “topic”. The key has been accessed, so we should increment the access counter for the key. FrequencyCounter is a shared data structure, so an option to increment the access counter is to take a lock on the entire data structure and then increment the count. If multiple threads try to increase the access count for the same or different keys, all these threads would be contending for a single write lock on FrequencyCounter.

This is where the paper BP-Wrapper comes in. This paper suggests two ways of dealing with contention prefetching and batching.

CacheD uses batching with get and put operations.

Get

A get operation returns the value for a key if it exists. It queries the Store and gets the value. The next step in get is to increase the access count for the key. This is where the idea of batching comes in. All the gets are batched in a ring-buffer-like abstraction called Pool . Pool is a collection of Buffer and each Buffer is a collection of hashes of the keys.

Any time a key is accessed, it is added to a buffer within the Pool. When a buffer is full, it is drained. Draining involves sending the entire Vec<KeyHash> to a BufferConsumer . BufferConsumer is implemented using a single thread that receives the buffer content from a channel . The BufferConsumer on receiving the buffer content applies it to the FrequencyCounter, thereby incrementing the frequency access of the entire set of keys. The channel size is kept small to reduce contention and the memory footprint of collecting the buffer in memory. If the channel is full, the buffer content is dropped.

AdmissionPolicy plays the role of BufferConsumer in CacheD.

The current implementation of CacheD uses a fine-grained lock over each buffer: buffers: Vec<RwLock<Buffer<Consumer>>>. The next release may change this implementation.

Put

The idea with get was to buffer the accesses and apply them to the FrequencyCounter when the buffer gets full. We can not use the same idea with put because we want to serve the put operations as soon as possible. However, batching is still relevant with put (or any other write) operations.

The idea is to treat every write operation (put, update, delete) as a command, send it to a mpsc channel and have a single thread receive commands from the channel and execute them one after the other.

CacheD follows the same idea. Every write operation goes as a Command to the CommandExecutor . CommandExecutor is implemented as a single thread that receives commands from a crossbeam-channel . Every time a command is received, it is executed by this single thread of execution.

This design choice has obvious implications.

The solution to both these points lies in providing the right feedback to the clients. CacheD provides CommandAcknowledgementHandle as an abstraction that implements the Future trait. Every write operation is returned an instance of CommandSendResult that wraps CommandAcknowledgement, which provides a handle() method to return a CommandAcknowledgementHandle to the clients.

Clients can perform await on the CommandAcknowledgementHandle and get the CommandStatus .

#[tokio::main]
 async fn main() {
    let cached = CacheD::new(ConfigBuilder::new(100, 10, 100).build());
    let status = cached.put("topic", "microservices").unwrap().handle().await;
    assert_eq!(CommandStatus::Accepted, status);
}

We have most of the building blocks for our cache; let’s now jump to the metrics collection in the cache.

Measuring metrics

At the end of the day, we would like to know how our cache is behaving. We want to collect counter-based metrics like CacheHits, CacheMisses, KeysAdded, KeysDeleted etc.

Let’s assume there are 16 such metrics that we want to collect. To do that, we can design a simple ConcurrentStatsCounter that can maintain an array of 16 entries, and each array element is of type AtomicU64. Whenever an event happens, like a key getting added to the cache, we increment its corresponding counter.
This approach can be represented with the following code:

const TOTAL_STATS: usize = 16;

#[repr(usize)]
#[non_exhaustive]
#[derive(Copy, Clone, Eq, PartialEq, Hash, Debug)]
pub enum StatsType {
   KeysAdded = 0,
   KeysDeleted = 1,
   //+ others
}

pub(crate) struct ConcurrentStatsCounter {
   entries: [AtomicU64; TOTAL_STATS],
}

pub(crate) fn add_key(&self) { self.add(StatsType::KeysAdded, 1); }

fn add(&self, stats_type: StatsType, count: u64) {
   self.entries[stats_type as usize].fetch_add(count, Ordering::AcqRel);
}

The approach looks excellent. However, we need to understand the concept of false sharing before concluding on the approach’s greatness.

False sharing

The memory in the L1, L2, L3 and L4 processor cache is organized in units called “cache lines”. The cache line is the smallest data transfer unit between the main memory and the processor cache. If the cache line size is 64 bytes, then a contiguous block of 64 bytes will be transferred from RAM to the processor cache for processing. The size of cache lines varies based on the type of the processor. For example, on x86-64, aarch64, and powerpc64, cache line is 128 bytes .

Updating an atomic value invalidates the whole cache line it belongs to.

Let’s go back to our code now. Let’s assume that the cache line size is 64 bytes. We have an array of AtomicU64; each AtomicU64 takes 8 bytes of memory. Our cache line size is 64 bytes, that means eight AtomicU64 values will lie in one cache line.

Let’s imagine that thread1 running on core-1 will update the atomic value at index 0 and thread2 running on core-2 will update the atomic value at index 1. We know that these atomic values lie on the same cache line, and “updating an atomic value invalidates the whole cache line it belongs to”. Invalidating a cache line will result in fetching that chunk of memory from RAM again.

Consider that thread1 running on core-1 updates the atomic value at index 0, invalidating the entire cache line that this value belongs to. Now, thread2 running on core-2 needs to update the value at index 1, but the entire cache line is invalidated. So, the cache line (64 bytes) needs to be fetched from RAM. Reading/Writing from/to RAM is in the order of 80-100 ns compared to the same from L1, L2, L3 and L4 cache, which is in the order of 1-10 ns.

thread2 running on core-2 updates the atomic value at index 1 after the cache line is fetched. This update invalidates the entire cache line again and forces another fetch of the cache line from RAM. This fetch/re-fetch/re-re-fetch of the cache line is courtesy of “false sharing”.

We are using “atomics” to ensure that each thread updates its value atomically, and because these values are on the same cache line, both the threads running on different cores end up sharing the same cache line for writing. This increases latency because of the repeated fetch of the cache line(s) from RAM. This is called “false sharing”. Imagine the extent of the problem with 128 cores.

The way to deal with “false sharing” is to pad the values so that each AtomicU64 lies on its cache line. One option is to pad the values manually, and the other is to use a library that can help with padding. CacheD uses CachePadded to pad the values.

With the introduction of CachePadded, this is how the code looks like:

const TOTAL_STATS: usize = 16;

#[repr(usize)]
#[non_exhaustive]
#[derive(Copy, Clone, Eq, PartialEq, Hash, Debug)]
pub enum StatsType {
   KeysAdded = 0,
   KeysDeleted = 1,
   //+ others
}

#[repr(transparent)]
#[derive(Debug)]
//introduce a new abstraction that wraps AtomicU64 inside CachePadded
struct Counter(CachePadded<AtomicU64>);

//entries now contains Counters instead of AtomicU64
//each Counter is a CachePadded AtomicU64
//therefore, each AtomicU64 is now placed on its own cache line
pub(crate) struct ConcurrentStatsCounter {
   entries: [Counter; TOTAL_STATS],   
}

pub(crate) fn add_key(&self) { self.add(StatsType::KeysAdded, 1); }

fn add(&self, stats_type: StatsType, count: u64) {
   //fetch_add is now available in Counter
   self.entries[stats_type as usize].0.fetch_add(count, Ordering::AcqRel); 
}

We are done with all the building blocks :). Great job. Let’s understand a way to measure the cache-hit ratio.

Measuring cache-hit ratio

Hit ratio is defined by the following formula:

Hit ratio = number of hits/(number of hits + number of misses) 
or 
Hit ratio as percentage = (number of hits/(number of hits + number of misses)) * 100

Let’s understand the problem better. We need the following:

  1. A distribution of elements of type T. We will be performing get and put operations using the elements of this distribution. The distribution:
    • should consist of values (/elements) within the specified range
    • should have some way of defining the repetition of elements (some elements should occur M times, some should occur P times, while some should occur just one time)
  2. For each element, perform a get operation in the cache
    • This results in measuring the hits and misses
  3. If the element is not present, perform a put operation in the cache
    • This results in adding a new element from the distribution in the cache

Distribution of elements

The distribution of elements is a collection of N elements of type T that will be loaded in the cache via put operation and the elements from this distribution will be queried from the cache via get operation. This distribution should be able to repeat elements based on some logic.

Let’s take a look at Zipf's law .

Zipf’s law often holds, approximately, when a list of measured values is sorted in decreasing order. It states that the value of the nth entry is inversely proportional to n. The best known instance of Zipf’s law applies to the frequency table of words in a text or corpus of natural language. Namely, it is usually found that the most common word occurs approximately twice as often as the next common one, three times as often as the third most common, and so on. For example, in the Brown Corpus of American English text, the word “the” is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf’s Law, the second-place word “of” accounts for slightly over 3.5% of words (36,411 occurrences), followed by “and” (28,852). (Referenced from ).

If the words are ranked according to their frequencies in a large collection, then the frequency will decline as the rank increases, so a small number of items appear very often, and a large number rarely occur. (Reference ).

This idea matches what we want. We can use the Zipf distribution to check cache hits because it will cause some elements to appear frequently while others will appear rarely. In the rust ecosystem, the crate rand_distr provides the Zipf distribution.

We have the distribution part sorted out. Now, we can write a benchmark that loads K elements of the distribution in a cache with weight W. All we need to do is identify K and W.

The idea is to have a large enough distribution sample, and CacheD uses a distribution size of 16 * 100_000, which means the Zipf distribution will contain 16 * 100_000 elements with the biggest value as 16 * 100_000. So, our K = 16 * 100_000.

Each key/value pair that is being loaded is of type u64, and the weight of a single key/value pair is 40 bytes.

We want the cache weight to be less than the total weight of the incoming elements to simulate rejections . We keep the cache weight to be 1/16th of the total weight of the incoming elements. That means the cache weight (W) = 100_000 * 40 bytes. That’s it; we are now ready to run the benchmark .

/// Defines the total number of key/value pairs that may be loaded in the cache
const CAPACITY: usize = 100_000;

/// Defines the total number of counters used to measure the access frequency.
const COUNTERS: TotalCounters = (CAPACITY * 10) as TotalCounters;

/// Defines the total size of the cache.
/// It is kept to CAPACITY * 40 because the benchmark inserts keys and values with weight 40.
const WEIGHT: Weight = (CAPACITY * 40) as Weight;

/// Defines the total sample size that is used for generating Zipf distribution.
/// Here, ITEMS is 16 times the CAPACITY to provide a larger sample for Zipf distribution.
/// W/C = 16, W denotes the sample size, and C is the cache size
const ITEMS: usize = CAPACITY * 16;

pub fn cache_hits_single_threaded_exponent_1_001(criterion: &mut Criterion) {
   criterion.bench_function("Cached.get()", |bencher| {
      let runtime = Builder::new_multi_thread()
              .worker_threads(1)
              .enable_all()
              .build()
              .unwrap();

      bencher.to_async(runtime).iter_custom(|iterations| {
         async move {
            let cached = CacheD::new(ConfigBuilder::new(COUNTERS, CAPACITY, WEIGHT).build());
            let distribution = distribution_with_exponent(ITEMS as u64, ITEMS, 1.001); //Zipf exponent

            let hit_miss_recorder = HitsMissRecorder::new();
            let mut index = 0;

            let start = Instant::now();
            for _ in 0..CAPACITY*16 {
               let option = cached.get(&distribution[index]);
               if option.is_some() {
                  hit_miss_recorder.record_hit();
               } else {
                  hit_miss_recorder.record_miss();
               }
               cached.put_with_weight(distribution[index], distribution[index], 40).unwrap().handle().await;
               index += 1;
            }
            cached.shutdown();
            println!("{:?} %", hit_miss_recorder.ratio());
            start.elapsed()
         }
      });
   });
}

The result for cache-hits in CacheD is available here .

That’s it. We have all the building blocks needed to build an in-memory LFU cache.

Code

The source code of CacheD is available here and the crate is available here .

Relevant research papers

References

Cache

TinyLFU

CacheD